SHARE
Research Highlight

Variational Generative Flows for Reconstruction Uncertainty Estimation

Topic:

The Science
A research team from ORNL and Pacific Northwest National Laboratory has developed a deep variational framework to learn an approximate posterior for uncertainty quantification. For non-convex image construction problems, a deep architecture with sufficient expressivity is required. The framework in this work addresses two challenges:

  • The instability of deep architectures due to the aggregation of numerical noise in the data
  • The violation of the required invertibility of the normalizing flows architecture

The proposed model is based on bidirectional regularization, with the incorporation of gradient boosting to enhance the flexibility.

The Impact
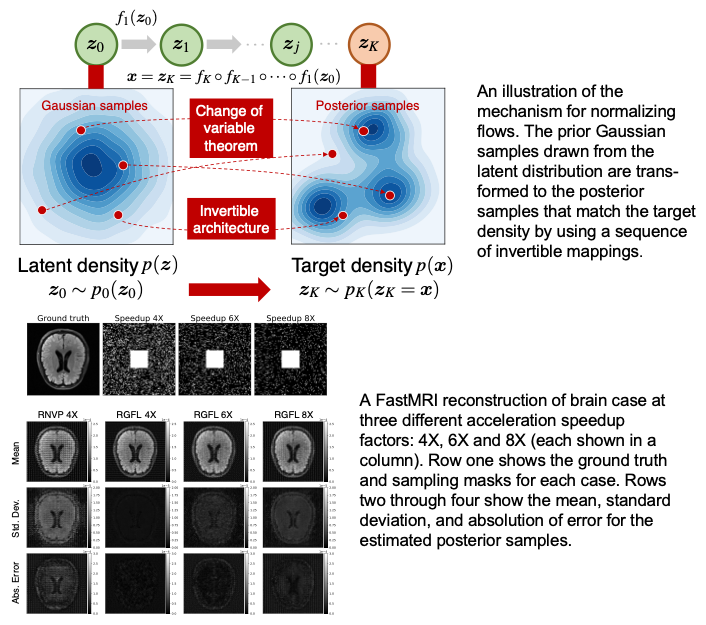
The effectiveness of the model is demonstrated through FastMRI reconstruction and interferometric imaging problems. The proposed method achieves a reliable and high-quality reconstruction with accurate uncertainty estimation.
 

Variational Generative Flows for Reconstruction Uncertainty Estimation CSMD Computer Science and Mathematics Division ORNL

PI/Facility Lead(s): Frank Liu
Publication(s) for this work:

  • J. Zhang, J. Drgona, S. Mukherjee, M. Halappanavar, and F. Liu, “Variational Generative Flows for Reconstruction Uncertainty Estimation.” International Conference on Machine Learning, July 18-24, 2021.

Team Members: Jiaxin Zhang, Frank Liu (ORNL), Jan Drgona, Sayak Mukherjee, Mahantesh Halappanavar (PNNL)

Summary
The goal of inverse learning is to find hidden information from a set of only partially observed measurements. To fully characterize the uncertainty naturally induced by the partial observation, a robust inverse solver with the ability to estimate the complete posterior of the unrecoverable targets conditioned on a specific observation is important and has the potential to probabilistically interpret the observational data for decision making. 

This work proposes an efficient variational approach that leverages a generative model to learn an approximate posterior distribution for the purpose of quantifying uncertainty in hidden targets. This is achieved by parameterizing the target posterior using a flow-based model and minimizing the Kullback-Leibler divergence between the generative distribution and the posterior distribution. Without requiring large training data, the target posterior samples can be efficiently drawn from the learned flow-based model through an invertible transformation from tractable Gaussian random samples.

Acknowledgement of Support
This material was based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Applied Mathematics program under contract and award numbers KJ0401 at Oak Ridge National Laboratory (ORNL) and under contract and award number 76815 at Pacific Northwest National Laboratory (PNNL). ORNL is operated by UT- Battelle, LLC., for DOE under Contract DE-AC05-00OR22725. PNNL is operated by Battelle Memorial Institute for DOE under Contract No. DE-AC05-76RL01830.